ここに9枚のカードがある。
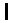
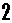
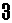
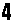
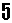
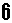
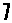

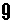
カードを横一列に並べて整数を表したい。但し、カードは互いに重ならないように配置し、またすべて使い切ること。
(1)表される最小の整数は何か?
(2)表される最小の正整数は何か?
頭の体操になった?
問、次の文の意味が矛盾しない様に( )内を整数で埋めなさい。
この文には0が( )個、1が( )個、2が( )個、3が( )個、4が( )個、
5が( )個、6が( )個、7が( )個、8が( )個、9が( )個、ふくまれている。
解答
a. 0-1個 1-7個 2-3個 3-2個 4-1個 5-1個 6-1個 7-2個 8-1個 9-1個
b. 0-1個 1-11個 2-2個 3-1個 4-1個 5-1個 6-1個 7-1個 8-1個 9-1個
解説
答えが2種類もあって、なかなかイヤラシイなあ。
解説はしません。偶然見つけたんで。1の個数がポイントかな?
外見が同じ9個の玉があります。この中に1つだけ、重い玉が混じっています。
天秤を2回だけ使い、どの玉が重いかを見つけなさい。
解答
まずは、[A] ●●● [B] ●●● [C] ●●● と分ける。
[B] と [C] を秤にのせる。(1回目)
これが釣り合えば、重い玉は [A] にある。不釣り合いなら、下がった方のグループに重い玉がある。
次に、重い玉があるグループを [X] ● [Y] ● [Z] ● と分ける。
[Y] と [Z] を秤にのせる。(2回目)
これが釣り合えば、重い玉は [X]。不釣り合いなら、下がった方が重い玉と結論できる。
解説
相対的な重さが分かっているので、3つに分けて内2つを比較すればおおよそ特定できるってことに気付けばおしまい。
9=3×3なので、2回比較すれば完全に決定できるって寸法。楽勝でしょ?
外見が同じ12個の玉があります。このなかに1つだけ重さの違う玉が混じっています。
天秤を3回だけ使って、その重さの違う玉を見つけなさい。
また、その重さの違う玉は、残りの11個に比べ、重いか軽いかも答えなさい。
解答
まず、3つのグループ [A] ●●●● [B] ●●●● [C] ●●●● に分ける。
[A] と [B] を秤にのせる。(1回目)
・釣り合う
[A]、[B] は普通の玉、[C] の中に重さの違う玉があると分かる。
[C] を2分して、[C] ●●● [C'] ● とする。
[A+B] から3つと [C] を秤にのせる。(2回目)
これが釣り合えば [C'] に、不釣り合いなら [C] に重さの違う玉がある。
釣り合った場合。重さを特定するだけでよいから、普通の玉と比較すればよい。
[A+B+C] から1つと [C'] を秤にのせる。(3-1回目)
[C'] が上がれば軽く、下がれば重いと判明する。
不釣り合いの場合。[C] が上がっていれば軽い玉、下がっていれば重い玉がある。(★)
重さが既知になったから [C] を3分すればよい。[X] ● [Y] ● [Z] ● と分ける。
[Y] と [Z] を秤にのせる。(3-2回目)
これが釣り合っていれば、答えは [X]。重さは★で判断できる。
不釣り合いならば、★と同じ振るまいをする方の玉が求める答えとなる。
・不釣り合い
この場合、[A] か [B] に重さの違う玉があり、[C] は普通の玉である。
今、下に傾いた方のグループを [B] と考えても差し支えない。
従って、重さの違う玉が [A] にあればそれは軽く、[B] にあれば重いことが結論される。
では、玉の特定をしよう。次のようにグループを構成し直す。
[X] ●●●○ … [C]×3+[B]×1
[Y] ●●●○ … [B]×3+[A]×1
[Z] ●●●○ … [A]×3
[X] と [Y] を秤にのせる。(2回目)
釣り合った場合。[Z] の中に軽い玉がある。[Zx] ● [Zy] ● [Zz] ● と分ける。
[Zy] と [Zz] を秤にのせる。(3-1回目)
これが釣り合えば、[Zx] が答え。釣り合わなければ、上がった方が答えである。
不釣り合いの場合。次の2つの可能性がある:[X] が下がる [Y] が下がる
[X] が下がった場合。
このとき、[X] の○が重いか、[Y] の○が軽いかの一方のみ成り立つ。[Z] は普通の玉である。
[Y] の○と [Z] の1つを秤にのせる。(3-2回目)
これが釣り合えば、[X] の○が重く、釣り合わなければ [Y] の○が軽い。
[Y] が下がった場合。
このとき、[X] と [Y] の構成から考えて、重さの違う玉は [Y] にある。
つまり、[Y] の●×3の中に重い玉があることが分かる。これを [Yx] ● [Yy] ● [Yz] ● と分ける。
[Yy] と [Yz] を秤にのせる。(3-3回目)
これが釣り合えば、[Yx] が答え。不釣り合いならば、下がった方が答え。
解説
問題02の応用問題。重さも未知なる天秤の問題。
重さが違う可能性のある玉を3つ以下に絞る工夫が試されていると思う。
ポイントは、12=4×3、4=3+1か。
3つ以下になれば、あと1回で特定できる訳だから、2回目をどうするかが重要。
普通の玉と混合させて、3+1を作るのがミソだと思う。
解答、分かりやすいかしら?
はじめに1という数がある。
次の数は
1:前の数に2をかけてから1をたす
2:前の数に1をたしてから2をかける
のどちらかを自由に選んで作る。このとき
(1)100を作ることができるか。
(2)1000を作ることができるか。
(3)10のn乗(nは自然数)はどんな時に作る事が出来るか?
解答
(1)できない (2)できない (3)特定不可?
解説
自然数mに対して、操作1で 2m+1、操作2で 2m+2 が作れる。
この逆の操作を考える。具体的に与えられた自然数Mに対して、
Mが奇数のとき、操作1':Mから1を引いて2で割る
Mが偶数のとき、操作2':Mから2を引いて2で割る
これにより、Mの1つ前の数字が得られる。
操作1と操作2の逆の操作によって数字を小さくしていけば、いずれ「1」か「2」に行き着く。
もし、Mから「2」が得られたなら、Mは操作1と操作2で「1」から作ることができない。
100 → 49 → 24 → 11 → 5 → 2
1000 → 499 → 249 → 124 → 61 → 30 → 14 → 6 → 2
だから、「1」からは作れない。
(3)はnの特徴づけを問うている。
特徴が仮にあったとしても、分かりやすい形には書けない。まあ、特別に注目すべき特徴はないだろう。
少し、補足。
与えられた自然数mを2進展開する。そのとき、m+1=10*****_[2] となれば「1」からmが作れる。
逆に、「1」から作れる数字mは、2進展開したとき m+1=10*****_[2] となる。
このことから
66…6(6がn個並ぶ)<m<10^n を満たすm=2^kが存在すれば、10^nは「1」から作れる
ことが分かる。これなら、電卓でも2のベキを計算させるだけで簡単に判定できる。
ちなみに、10^nが「1」から作れるようなnの割合はlog(3/2)÷log2=約58.5%。
ここに9枚のカードがある。
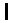
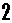
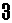
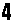
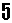
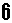
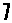

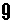
カードを横一列に並べて整数を表したい。但し、カードは互いに重ならないように配置し、またすべて使い切ること。
(1)表される最小の整数は何か?
(2)表される最小の正整数は何か?
解答
(1)-99875432 (2)3
解説
カードの扱いと問題文の「整数を表す」がポイント。式で整数を表してもよい、と解釈できないと(2)はいつまでも解けない。
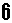
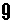 は、180度回転させれば「9」にも「6」にもなる。
は、180度回転させれば「9」にも「6」にもなる。 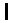 を「1」と思わないで、90度回転させれば
を「1」と思わないで、90度回転させれば  で「-(マイナス、引く)」となり、少し回転させれば
で「-(マイナス、引く)」となり、少し回転させれば 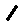 で「/(割る)」となる。この扱いは重要。
で「/(割る)」となる。この扱いは重要。
(1)一番大きな数を作ってマイナス(つまり1のカード)を添えればよい。 
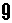
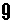

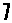
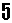
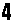
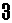
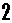 が最小だよん。
が最小だよん。
(2) 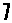
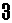
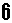

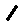
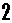
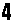
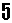
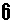 または
または 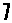
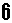
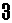

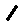
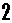
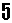
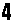
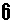 より、「3」は作れる。「1」や「2」は作れないから「3」が最小。
より、「3」は作れる。「1」や「2」は作れないから「3」が最小。
意外に多そうなのは(2)で、「6523−6487」のように引き算で答えを出すことかな。
夢人都市に戻る